1. مدخل سهل إلى تلخيص البيانات

في هذا الدرس، سنعرّف ببعض المصطلحات والمفاهيم المعتمدة، بما فيها تلك المتعلقة بالأنواع أو الفئات الأساسية للبيانات، قبل أن نتعلّم كيفية وصف مجموعة معيّنة من البيانات. فنصبح جاهزين في الختام لتبنّي المفاهيم الواردة هنا، واستخدامها لتلخيص قائمة مكاتب الاقتراع في الوحدة اللاحقة.

المصطلحات المتعلقة بالبيانات

سنبدأ أولاً بفهم بعض المصطلحات المتداولة عند دراسة البيانات.

المشاهدات

تتضمّن أي مجموعة بيانات معلومات عن “individuals” (عناصر فردية)، كل عنصر منها يُسمّى “observation” (مشاهدة) أو “case” (حالة). ويتضمّن كل صف في معظم تلك المجموعات معلومات عن عنصر معيّن. في الوحدة 1، عاينّا قائمةً لمكاتب الاقتراع، كان كل صف من مجموعة بياناتها يتضمّن معلومات عن مكتب اقتراع فردي.

المتغيّرة

تُدعى كل ميزة من ميزات العنصر الفردي (أي المشاهدة) متغيّرة. وتتيح بعض المتغيّرات، مثل النوع الاجتماعي والوظيفة، تضنيف الأفراد بكل بساطة ضمن فئات، فيما تأخذ أخرى، كالطول أو عدد الناخبين المسجّلين، شكل قيمة عددية تُقدّر بموجب عملية حسابية. في المرحلة اللاحقة، سندرس عن كثب مختلف أنواع البيانات.

أنواع البيانات

يتمّ تخزين البيانات بعدة أشكال وأنواع، يُشار إليها أحياناً “level of measurement” بـ(مستويات القياس). علينا أن نفهم نوع البيانات لأنه يساعدنا في معرفة كيفية تلخيصها بشكل صحيح. تتوزّع البيانات على ثلاثة أنواع:

1. البيانات الفئوية أو الإسمية: وهي البيانات التي تندرج ضمن عدة فئات ولا تأخذ شكلاً عددياً (كالنوع الاجتماعي، والانتماء الإثني، والدوائر الانتخابية). قد تتضمّن الاستمارة المعدّة لمراقبة الانتخابات السؤال التالي مثلاً: "هل سُمح لك أن تراقب طوال اليوم؟"، والإجابة عنه تحتمل إما "نعم" أم "لا". قد تنشر هيئة إدارة الانتخابات، من جهتها، قائمة بأسماء المسؤولين المعيّنين لكل مكتب اقتراع، تتضمّن إسمه ومنصبه. من المرجّح أن تتخذ متغيّرة “position” (المنصب) شكل بيانات موزّعة على فئات (أي رئيس، نائب رئيس، أمين سر).
2. البيانات وفق ترتيب معيّن: وهي بيانات تندرج ضمن فئات تخضع لترتيب أو تسلسل معيّن. تطرح استمارات متعددة لمراقبة الانتخابات مثلاً السؤال التالي: "كم عدد الناخبين الذين تلقّوا مساعدة عند التصويت؟" الإجابة عن هذا السؤال تتراوح بين "لا أحد"، "عدد قليل"، "البعض"، أو "عدد كبير". فالـ"عدد الكبير" يفوق "البعض" الذي يكون أكثر من "لا أحد".
3. البيانات المتواصلة أو المتقطعة: يشير هذا النوع من البيانات إلى سلسلة متتابعة من الأرقام، يمكن أن تَرِد فيها جميع قيم البيانات. قد تتضمّن الاستمارة المعدّة لمراقبة الانتخابات سؤالاً عن عدد الناخبين المسجّلين في كل مكتب اقتراع أو عدد الأصوات التي يحصل عليها كل مرشح.

عندما نفهم أولاً أنواع البيانات التي تشكّل محور المتغيّرة، نستطيع أن نختار أفضل وسيلة لتلخيص تلك المتغيّرة، أو وصفها.

وصف البيانات وتلخيصها

لماذا نلخّص البيانات؟ نلخّص البيانات بهدف “simplify” (تبسيطها)، والتمييز بسرعة بين ما كان منها “normal” (طبيعياً) وغير طبيعي. ويتبيّن من طريقة توزيع المتغيّرة القيم التي تكتسبها، وكم مرة تكتسبها.

لعلّ أكثر وسيلتين مفيدتين لوصف توزيع البيانات هما:

1. الطريقة المعهودة: التي تصف محور، أو مركز، البيانات. وتُعرَف أيضاً “measure of central tendency” (بمقياس النزعة المركزية).
2. طريقة تشتّت القيم حول النقطة المركزية، وهي تشير إلى مدى كثافة البيانات الموزّعة حول تلك النقطة. وتُعرف أيضاً “measure of dispersion” (بمقياس التشتّت).

يُشار إلى هاتين الوسيلتين أيضاً بالإحصاءات الوصفية.

1. المركز: ما هو النموذجي؟ (النزعات المركزية)

يمكن مراقبة النقطة المركزية بثلاث وسائل شائعة، وهي الوسط الحسابي (المسّى أيضاً المتوسط) والنمط، و الوسيط. وتلخّص ثلاثتها معاً توزّع البيانات من خلال وصف القيمة النموذجية للمتغيّرة (الوسط الحسابي)، أو العدد الأكثر تكراراً (النمط)، أو العدد الذي يتوسّط جميع الأرقام الأخرى المدرجة ضمن مجموعة بيانات (الوسيط).^[1] في هذه الوحدة، سنركّز على الوسط الحسابي، الذي يعدّ الوسيلة الأنسب لقياس محور البيانات المتقطعة/المتواصلة (كعدد الناخبين المسجّلين). لاحتساب هذا المعدل، نجمع جميع الأرقام العائدة للمتغيّرة، قبل أن نقسمها على عددهم. بعبارة أخرى، الوسط الحسابي (المتوسط) هو مجموع القيم مقسوماً على عددها.

مثال بسيط

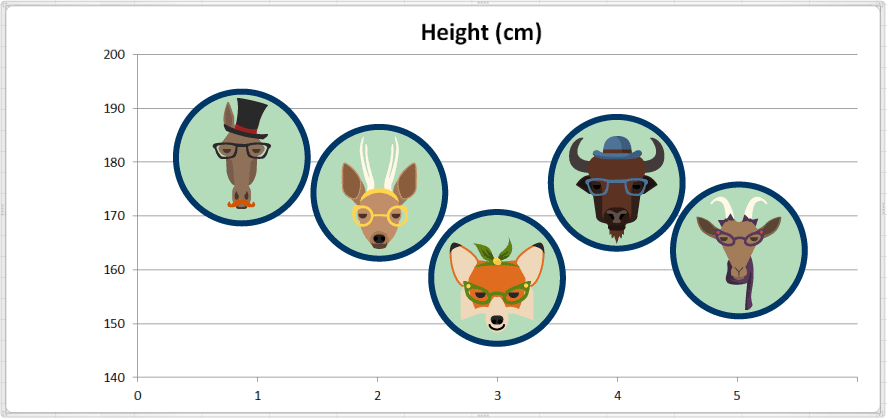
تتضمّن مجموعة البيانات النموذجية المبيّنة أدناه معلومات عن أسماء بعض الحيوانات، إضافة إلى قياس طول كل حيوان. وتحتوي على متغيّرتين، وهما “name” (الإسم) و“height” (الطول)، إضافة إلى خمس مشاهدات. إليك في ما يلي مجموعة البيانات:

أعددنا هنا رسماً بيانياً سريعاً يعيّن طول كل حيوان:

لاحتساب متوسط الطول (بالسم)، نجمع جميع القيم، ثمّ نقسمها على إجمالي عدد المشاهدات:

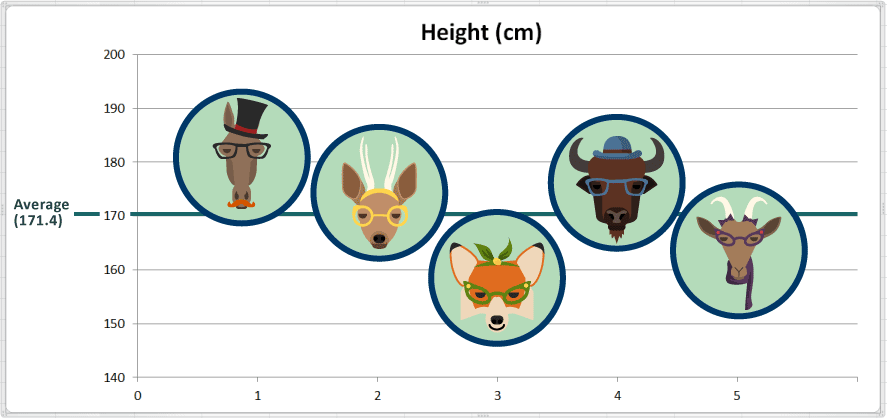
متوسط الطول = (181 + 175 + 159 + 177 + 165) ÷ 5 = 857 ÷ 5 = 171.4

يتبيّن ممّا تقدّم أنّ متوسط قيمة الطول يبلغ 171,4 سنتمترات. وقد أضفنا في هذه المرحلة خطاً متمايزاً للدلالة على موقع هذا المتوسط في الرسم البياني الذي أعددناه، لتنتبه إليه:

2. تشتّت البيانات: كيف تتوزّع البيانات حول النقطة المركزية؟ (مقاييس الانتشار)

إنّ دراسة طريقة توزّع البيانات تطلعنا على حجم الاختلاف أو التنوّع بين البيانات. أما المقاييس الثلاثة المعتمدة في احتساب طريقة توزّعها فتتمثّل في تحديد المدى، والانحراف المعياري، والتباين.

المدى

هو الفارق بين أعلى قيمة وأدناها، والمسافة بين حدّين. لاحتساب هذه القيمة، نقوم بطرح الحدّ الأدنى من الحدّ الأقصى.

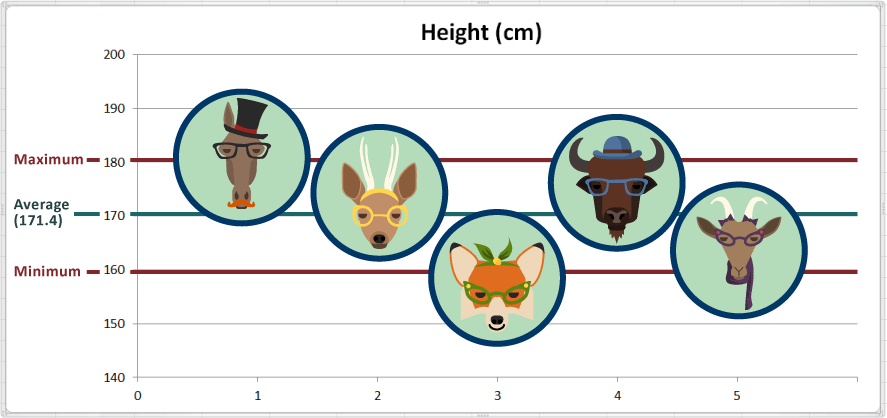
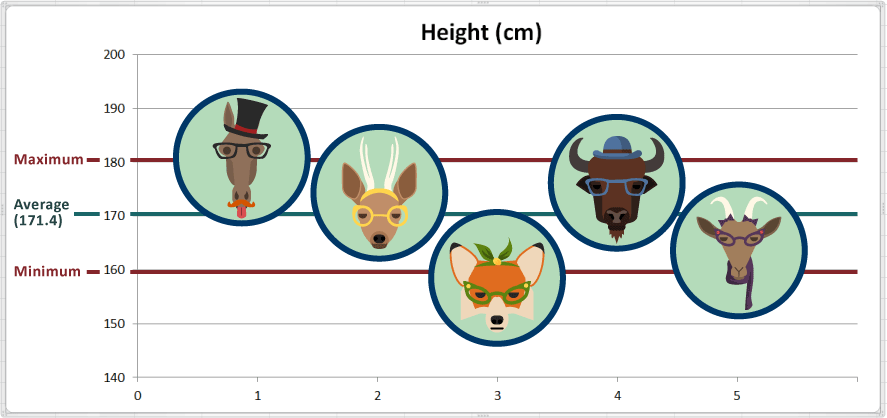
في مجموعة البيانات التي نستند إليها، ما هي أعلى قيمة “maximum” ("الحدّ الأقصى")؟ 181 سم في المثال عينه، ما هي أدنى قيمة “minimum” ("الحدّ الأدنى")؟ 159 سم لذا، فإنّ المدى الذي تسجّله مجموعة البيانات القليلة حول قياس الطول هي 181 – 159 = 22 سم أضفنا في هذا الإطار بعض الخطوط المتمايزة إلى الجدول للدلالة على الأعلى “maximum” ("الحدّ الأقصى") و“minimum” الأدنى ("الحدّ الأدنى"):

من الناحية العملية، يصنّف الحيوان الذي سجّل أعلى قيمة بالحيوان الأطول، والحيوان الذي سجّل أدنى قيمة بالحيوان الأقصر. بالتالي نستنتج أنّ الحصان هاري هو الأطول، فيما الثعلب فران هو الأقصر.

يزوّدنا حساب المدى بالحدّين (أي النقيضين)، لكنه لا يعطينا فكرة عن مدى تقارب أو تباعد البيانات عند توزّعها بين هذين الحدّين. ولا نعلم أيضاً إذا كانت تلك البيانات هي بأكثرها أقرب إلى الوسط الحسابي، أو الحدّ الأقصى، أو الحدّ الأدنى. يتبيّن من الجدول الذي نعتمده أنّ ما يزيد عن نصف الحيوانات هي طويلة (أي أعلى من متوسط الطول).

من شأن مقياسين آخرين مرتبطين بطريقة انتشار البيانات، أي التباين والانحراف المعياري، أن يساعداننا في الإجابة عن تلك الأسئلة، إذ يلخّصان بالأرقام مدى تشتّت البيانات.

الانحراف المعياري

يوفّر الانحراف المعياري “standard deviation” ("الانحراف المعياري") وسيلة قياسية لمعرفة ما هو عادي^[2] بالاستناد إلى الوسط الحسابي. لعلّ أكثر ما يفيد فعلياً في سمات الانحراف المعياري هو أنه يعتمد نفس وحدات قياس البيانات. هو أشبه بمؤشر التقلّبات لأنه يُحدد بالتناسب مع حجم تشتّت البيانات. يسجّل الانحراف المعياري أعلى درجاته عندما تكون البيانات متباعدة جداً عن بعضها البعض (أي تكون البيانات شديدة التشتّت)، وأدناها عندما تكون البيانات متقاربة من بعضها البعض (أي تكون البيانات شديدة التمركز).

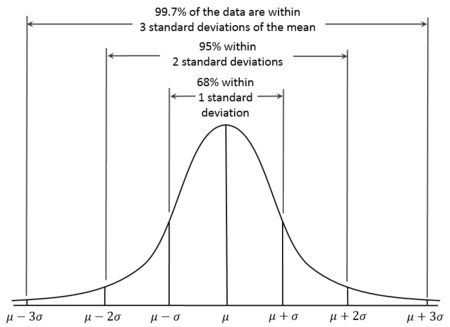
يساعد الانحراف المعياري كثيراً في فهم مدى تشتّت المتغيّرة. بالنسبة إلى معظم البيانات الموزّعة بطريقة عادية، تتراوح جميع القيم تقريباً، وبشكل عام، بين ثلاث انحرافات معيارية عن الوسط الحسابي. وهذا ما يُعرف في علم الإحصاءات بقاعدة 68-95-99,7. يقع نحو 68,27% من القيم ضمن نطاق انحراف معياري واحد عن الوسط الحسابي (المتوسط). في خط موازٍ، يقع 95,45% من القيم تقريباً ضمن انحرافين معياريين عن المتوسط، فيما يقع ما يقارب (99,73%) من القيم ضمن ثلاثة معيارات انحرافية عن المتوسط.

مخطط بياني مستمدّ من ويكيبيديا حول قاعدة 68-95-99,7

في الوحدة 3، نستخدم برنامج آكسيل من أجل تلخيص البيانات المدرجة ضمن قائمة مكاتب الاقتراع لعام 2008.

في نموذج مجموعة البيانات حول قياس طول الحيوانات، احتسبنا الانحراف المعياري لمجمل مقاييس الطول، الذي بلغ 9,1 سم^[3]. وظلّلنا تلك المنطقة في الجدول لإبراز البيانات الواقعة ضمن الانحرافات المعيارية الثلاثة (9,1 × 3) عن الوسط الحسابي، حيث تُعدّ عادية كل بيانات تتراوح ضمن تلك الانحرافات.

يوفّر الانحراف المعياري وسيلة موحّدة لمعرفة ما يندرج ضمن خانة الطبيعي والعادي، وما يعتبر بالغ الطول أو القصر. نحن نعلم أنّ الثعلب فران هو قصير. عندما نتوقّف عند الانحراف المعياري، ونلاحظ أنّ ما يقارب جميع (99,73%) من إجمالي القيم يقع ضمن الانحرافات المعيارية الثلاثة، نستخلص أنّ فران قصير، إنما قصره طبيعي.

التباين

يقيس التباين، على مثال الانحراف المعياري، مدى تقارب أو تباعد القيم عن وسطها الحسابي. بالتالي، يشير التباين الأعلى إلى أنّ البيانات هي متباعدة جداً عن هذا المعدل، والأدنى إلى أنها متقاربة جداً منه. يساوي التباين متوسط مربعات اختلافات (أو انحرافات) كل قيمة عن وسطها الحسابي (تجد صيغتها الرياضية في نهاية هذه الملاحظة). لن نركّز على تلك الصيغة في هذه الوحدة، ولكن من المهم أن تعرف أنّ التباين هو نقطة الانطلاق لاحتساب الانحراف المعياري.

إختبر نفسك

اختبر معارفك من خلال الإجابة عن الأسئلة التالية:

1. ما المقصود بعبارة المشاهدة؟
2. ما الترابط القائم بين عبارتي "المشاهدات" والمتغيّرة؟
3. ما الغاية من وصف أو تلخيص مجموعة بيانات؟
4. ما هي أنواع البيانات الثلاثة (المسمّاة أيضاً مستويات القياس)؟
5. عدّد أكثر وسيلتين مفيدتين لوصف طريقة توزيع البيانات.
6. هل قصر الثعلب فران غير طبيعي؟

استكشف البيانات

إذا أردت إجراء حساباتك الخاصة، إليك مجموعة بيانات الطول، علماً أنّ البيانات، إلى جانب بعض العمليات الحسابية، هي متوافرة على شكل ملف آكسيل أو ملف جداول البيانات المفتوحة.

صيغ رياضية

إليك في ما يلي الصيغتان الرياضيتان لاحتساب الانحراف المعياري، اللتين يتوسّع في شرحهما قسم صيغ الانحراف المعياري على موقع "الرياضيات تمرين مسلٍّ" الإلكتروني.

الانحراف المعياري لعدد السكان^[4]:

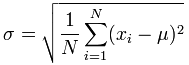
الانحراف المعياري للعيّنة:

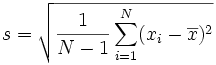
تبدو هاتان الصيغتان معقدتين، لكنّ التغيير الأهم يكمن في القسمة على N-1 (عوض N) عند احتساب التباين لعيّنة. (تذكّر أنّ الانحراف المعياري ما هو إلاّ الجذر التربيعي للتباين، ممّا يعني أنّ الصيغة المعتمدة لاحتساب التباين هي ذاتها الواردة أعلاه، إنما من دون شق الجذر التربيعي).

حقوق ملكية الصور والرسوم

تعود ملكية وحقوق جميع صور الحيوانات لشركة Dashikka/Shutterstock.

---

1. لاحتساب الوسيط، تُعتمَد الصيغة "(عدد نقاط البيانات] + 1) ÷ 2"، مع أنك لست ملزماً بتطبيقها. أو لعلك تكتفي بالعدّ من طرفي القائمة إلى أن تبلغ الوسط، إذا كنت تفضّل هذه الطريقة. أما النمطي فهو العدد الذي يتكرر أكثر من سواه. وبالتالي، ضمن سلسلة الأرقام 2، 3، 4، 5، 4، 4، 6، 10، 12، النمطي هو العدد 4. ↩︎

2. من المفيد أن نفهم عبارة عادي بمنطق الاحتمالات، حيث ترمز إلى ما هو ممكن للغاية أو مبدئي جداً. ↩︎

3. نهمل العملية الحسابية للانحراف المعياري في هذه الوحدة، لأننا نريد التركيز عليه كمفهوم، لا الغوض في صيغة احتسابه، علماً أنّ تلك الصيغة ومعدل التباين يتوافران في نهاية هذه الوحدة لمن يرغب في الاطّلاع عليهما. ↩︎

4. إنّ المصطلح "عدد السكان" يعني أنك تلخّص كامل (أي كل) مجموعة البيانات، فيما "العيّنة" تعني أنك تعمل على مجموعة صغيرة (أي عيّنة) من المجموعة الأوسع (أي مجمل عدد السكّان). ↩︎