1. Una breve introducción sobre cómo resumir datos
En este tutorial vamos a definir algunos términos y conceptos comunes, incluyendo los tipos o las categorías básicas(os) de datos. Luego aprenderemos a describir un conjunto de datos. Al finalizar este módulo, usted estará preparado para aplicar estos conceptos para resumir la lista de centros de votación en el siguiente módulo.
Términos de datos
Para comenzar aprenderemos algunos términos comunes empleados en el análisis de datos.
Observación
Un conjunto de datos contiene información acerca de "individuos" y a cada "individuo" se le llama "observación" o "caso".
Variable
Toda característica de un individuo (es decir, observación) se llama variable. Algunas variables, como son el género y el puesto, simplemente dividen a los individuos en categorías, mientras que otras, como la altura o el número de votantes registrados, asumen valores numéricos con los cuales se pueden realizar operaciones aritméticas. A continuación, veremos más a detalle los diferentes tipos de datos.
Tipos de datos
Los datos se almacenan como tipos distintos, a los que algunas veces se les denomina "nivel de medición". Es necesario entender el tipo de dato que se tiene porque esto nos ayuda a descifrar cuál es la mejor manera de resumirlo. Existen tres tipos de datos:
- Categóricos o nominales: Estos son datos que tienen distintas categorías y no son numéricos (por ejemplo: el género, la etnia, la circunscripción). Por ejemplo, un formulario de observación de elecciones podría incluir la pregunta: "¿Se le permitió observar todo el día?" y las opciones de respuesta serían "Sí" o "No". Un órgano de gestión electoral (EMB, por sus siglas en inglés), podría publicar una lista de funcionarios asignados a cada centro de votación, y esa lista podría contener el nombre y el puesto del funcionario. La variable de "puesto" probablemente será un dato categórico (por ejemplo: Presidente, Vicepresidente, y Secretario).
- Ordinales: Estos son datos con categorías que van en un orden o una jerarquía específicos. Por ejemplo, en muchos formularios de observación de elecciones hay preguntas como "¿Cuantas personas recibieron ayuda para votar?" donde las opciones de respuesta podrían ser: "Ninguna", "Pocas", "Algunas", o "Muchas". "Muchas" es más que "Algunas", que a su vez es más que "Ninguna".
- Continuos o de intervalo: Este tipo de datos tiene un rango continuo de números; todos los valores de datos son posibles. Por ejemplo, un formulario de observación de la jornada electoral podría pedir el número de votantes que hay registrados en cada centro de votación o el número de votos recibidos para cada candidato.
Si entendemos primero a qué tipo de dato corresponde una variable, podremos entonces decidir cuál es la mejor manera de resumir o describir esa variable.
Cómo describir y resumir datos
¿Por qué resumimos? Resumimos datos para "simplificarlos" e identificar rápidamente lo que parece "normal" y lo que parece extraño. La distribución de una variable muestra qué valores toma la variable y con qué frecuencia la variable toma esos valores.
Las dos maneras más útiles de describir la distribución de los datos son:
- La típica: Esto describe el centro o el punto medio de los datos. Esta manera de describir el centro también se conoce como "medida de la tendencia central".
- La dispersión de los valores alrededor del punto medio: Esto describe qué tan densamente están distribuidos los datos alrededor del centro. A esto también se le llama "medida de dispersión".
Estas dos maneras de describir los datos también se conocen como estadística descriptiva.
1. El punto medio: ¿Qué es típico? (Tendencias centrales)
Las tres maneras más comunes de ver el punto medio son: el promedio (también llamado media), la moda y la mediana. Los tres resumen la distribución de los datos al describir el valor típico de la variable (el promedio), el número que se repite con mayor frecuencia (la moda), o el número que está en medio de todos los demás números en un conjunto de datos (la mediana).[1] En este módulo nos vamos a enfocar en el promedio, ya que es la manera más adecuada de medir el centro de los datos de intervalo o continuos (por ejemplo, el número de votantes registrados). Para calcular el promedio se suman todos los números de una variable y luego se divide entre la cantidad total de números que hay. Dicho de otra manera, el promedio (la media), es la suma dividida entre el número total de observaciones.
Ejemplo sencillo
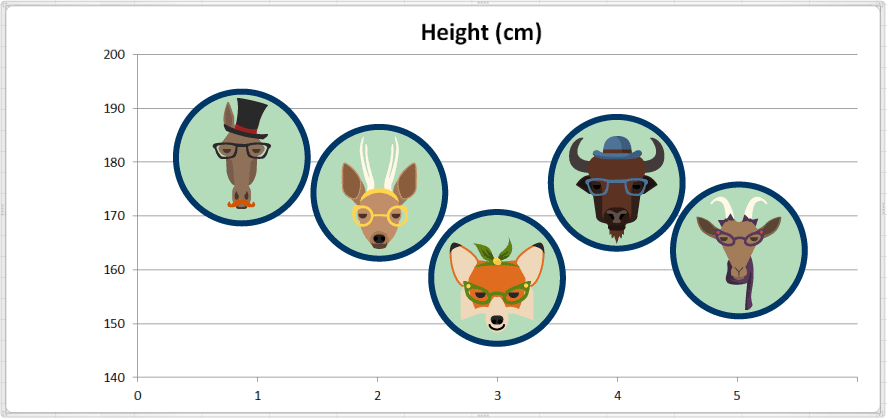
En el ejemplo del conjunto de datos que se muestra a continuación, tenemos información acerca de los nombres de ciertos animales. También tenemos las medidas de altura de cada animal. El conjunto de datos contiene dos variables: "name" (nombre) y "height" (altura), y cinco observaciones. Aquí está el conjunto de datos:
Hicimos una sencilla representación gráfica de la altura de cada animal:
Para calcular la Altura promedio (en cm) sumamos todos los valores y luego los dividimos entre el número total de observaciones:
Altura promedio = (181 + 175 + 159 + 177 + 165) ÷ 5 = 857 ÷ 5 = 171.4
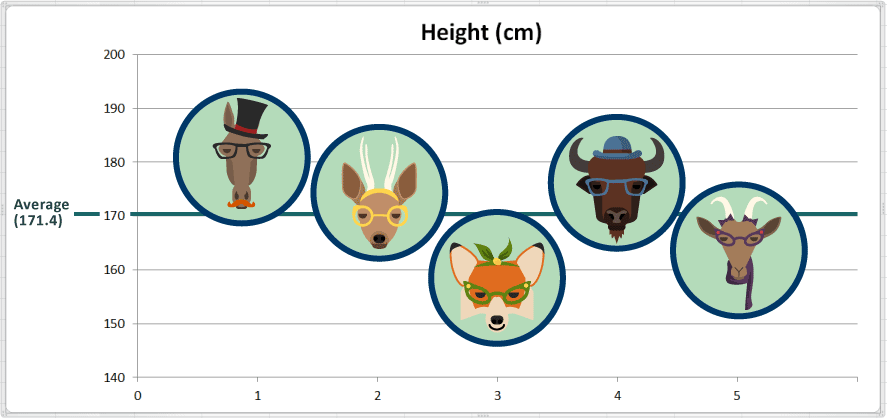
El valor promedio de la altura es 171.4 centímetros. En la siguiente gráfica agregamos una línea de referencia que marca el promedio para fines de comparación:
2. La dispersión: ¿Cómo están distribuidos los datos alrededor del punto medio? (Medidas de dispersión)
La extensión de la distribución de los datos nos indica el grado de variación, o diversidad, que existe en los datos. Las tres medidas de dispersión de los datos son el rango, la desviación estándar y la varianza.
Rango
Esta es la diferencia entre el valor más grande y el más pequeño; es la distancia que existe entre los extremos. Para calcular el rango, tomamos el valor máximo y le restamos el valor mínimo.
En nuestro conjunto de datos de altura, ¿cuál es valor más grande ("máximo")? 181 cm
En el mismo ejemplo, ¿cuál es el valor más pequeño ("mínimo")? 159 cm
El rango de nuestro pequeño conjunto de datos de alturas es entonces: 181 - 159 = 22 cm.
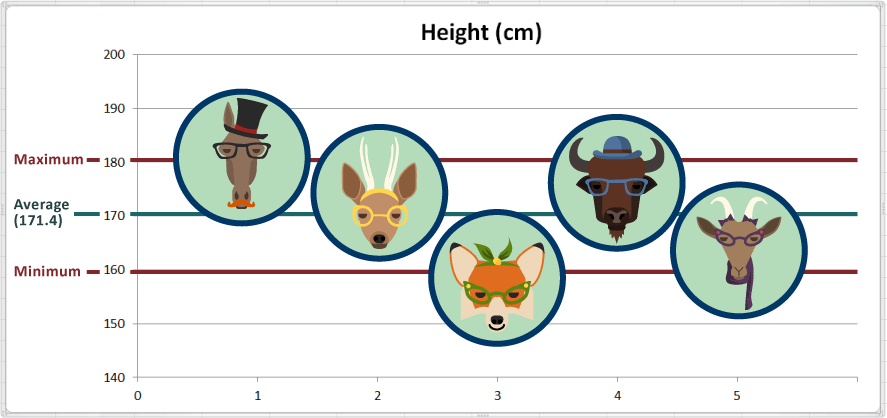
En la siguiente gráfica agregamos algunas líneas de referencia para indicar el "máximum" (máximo) y el "mínimum" (mínimo):
En términos prácticos, el animal con el valor máximo es el más alto, y el animal con el valor mínimo es el más bajo, de manera que, Harry the Horse (Harry el Caballo) es el más alto y Fran the Fox (Fran el Zorro) es el más pequeño.
Si bien el rango nos da los valores extremos, no nos dice nada acerca de cuán dispersa o concentrada es la distribución de los datos entre estos dos extremos. Tampoco sabemos si la mayoría de los datos se encuentran más cerca del promedio, del máximo o del mínimo. Por lo que vemos en la gráfica, pareciera que un poco más de la mitad de los animales son altos (es decir, por encima de la altura promedio).
Otras dos medidas de dispersión relacionadas (la varianza y la desviación estándar) nos pueden ayudar a responder estas preguntas, ya que ofrecen un resumen numérico de qué tan dispersos están los datos.
Desviación estándar
"Standard deviation" (la desviación estándar) nos ofrece una manera estándar de saber qué es lo normal[2] de acuerdo con el promedio. Un atributo muy útil de la desviación estándar es que se expresa en las mismas unidades que los propios datos. La desviación estándar es una especie de índice de variabilidad, porque es proporcional a la dispersión de los datos. Entre más diversa sea la distribución (es decir, cuando los datos están dispersos más ampliamente), más grande será la desviación estándar, mientras que entre menos diversa sea la distribución (es decir, cuando los datos están agrupados muy juntos), más pequeña será la desviación estándar.
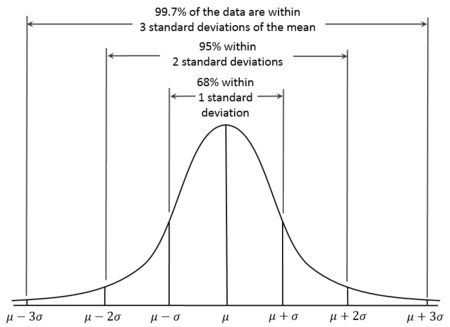
La desviación estándar es muy útil para entender el grado de dispersión de una variable. Para la mayoría de los datos distribuidos normalmente, generalmente casi todos los valores estarán dentro de tres desviaciones estándar del promedio. En la estadística, a esto algunas veces se le conoce como la regla del 68-95-99.7. Cerca del 68.27% de los valores están dentro de 1 desviación estándar del promedio (la media). De manera similar, aproximadamente el 95.45% de los valores se encuentran dentro de 2 desviaciones estándar de la media. Casi todos (99.73%) los valores están dentro de 3 desviaciones estándar de la media.
Diagrama de la regla 68-95-99.7 rule obtenido de Wikipedia
En el Módulo 3 usaremos Excel para resumir los datos contenidos en la lista de centros de votación de 2008.
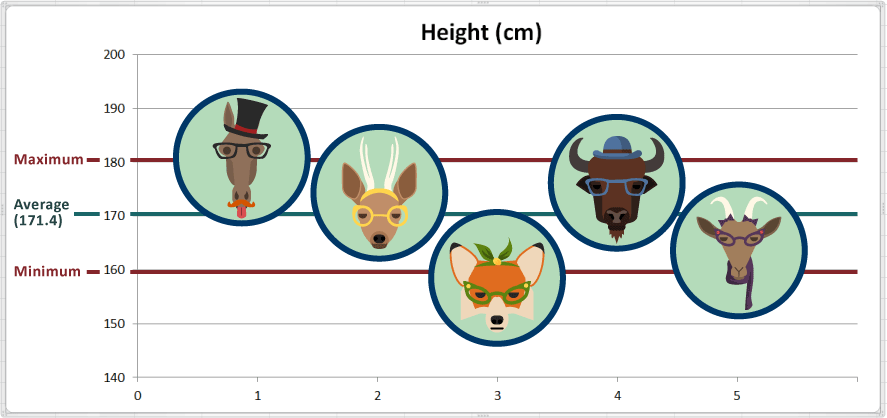
En el conjunto de datos de las alturas de los animales que tenemos como muestra calculamos la desviación estándar de las alturas, y el resultado[3] fue 9.1 cm. En la gráfica sombreamos el área para mostrar qué datos están dentro de 3 desviaciones estándar (9.1 x 3) del promedio. Todo dato que se encuentre dentro de este rango se considera normal.
La desviación estándar nos da una manera estandarizada de saber qué se considera normal, qué se considera muy grande o qué se considera muy pequeño. Sabemos que Fran el Zorro es pequeño, pero cuando consideramos la desviación estándar y que casi todos (99.73%) los valores están generalmente dentro de 3 desviaciones estándar, podemos concluir que Fran es pequeño, mas no anormalmente pequeño.
Varianza
De manera similar a la desviación estándar, la varianza mide qué tan estrecha o ampliamente dispersos están los números alrededor del promedio. De esta manera, una varianza grande significa que los datos están más alejados del promedio, y una varianza más reducida significa que están agrupados más cerca alrededor del promedio. La varianza es el promedio de las diferencias cuadradas (o desviaciones) de cada número con respecto al promedio (la fórmula matemática se encuentra al final de esta nota). En este módulo no nos vamos a enfocar en la fórmula, pero es importante entender que la varianza es la base para el cálculo de la desviación estándar.
Autoevaluación
Responda las siguientes preguntas para evaluar su conocimiento:
- ¿Qué es una observación?
- ¿Cómo se relacionan entre sí los términos "observaciones" y "variable"?
- ¿Cuál es el objetivo de describir o resumir un conjunto de datos?
- ¿Cuáles son los tres tipos de datos (también llamados "niveles de medición")?
- Enumere las dos maneras más útiles de describir la distribución de los datos.
- ¿Es Fran el Zorro anormalmente pequeño?
Juegue con los datos
Si quiere realizar sus propios cálculos, le proporcionamos el conjunto de datos de alturas. Los datos, junto con algunos cálculos, están disponibles como archivo de Excel o como archivo de hojas de cálculo de OpenOffice (Open Spreadsheets).
Fórmulas matemáticas
Aquí están las dos fórmulas para la desviación estándar que se explican en la sección de Fórmulas de la Desviación Estándar del sitio "Math is Fun" (Las matemáticas son divertidas).
La desviación estándar de la población[4]:
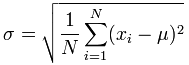
La desviación estándar de la muestra:
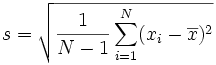
Parece complicado, pero el cambio importante es dividir entre N-1 (en lugar de N) cuando se calcula la varianza de una muestra. (Recuerde que la Desviación Estándar es tan solo la raíz cuadrada de la Varianza, así que la fórmula para calcular la varianza es la misma fórmula que se indica arriba pero sin la parte de la raíz cuadrada).
Créditos
Todos los derechos reservados de las imágenes de animales Dashikka/Shutterstock.
Para encontrar la mediana, la fórmula es ([el número de puntos de datos] + 1) ÷ 2, pero no es obligatorio usar la fórmula. Si lo prefiere, puede simplemente contar de afuera hacia adentro por ambos extremos de la lista hasta que llegue al centro. La moda es el número que se repite más que cualquier otro número. En la serie de valores: 2, 3, 4, 5, 4, 4, 6, 10, 12, la moda sería el 4. ↩︎
Es útil definir qué es normal en términos probabilísticos, donde lo normal significa algo que es altamente posible o muy típico. ↩︎
Nos saltamos el cálculo de la desviación estándar en este módulo porque queremos enfocarnos en ella como concepto y no quedarnos atorados en la fórmula. Las fórmulas de la desviación estándar y la varianza se incluyen al final de este módulo para aquellos que quieran verlas. ↩︎
El término "población" significa que se está resumiendo el conjunto de datos en su totalidad (es decir, completo). El término "muestra" significa que está trabajando con un subconjunto más pequeño (es decir, una muestra) del conjunto de datos más grande (es decir, la población). ↩︎