၁။ Data များကို အနှစ်ချုပ်ခြင်းအကြောင်း မိတ်ဆက်

ဤသင်ခန်းစာတွင် အချက်အလက်ကဏ္ဍ (data category) နှင့် အချက်အလက် အမျိုးအစားများ (types of data) အပါအဝင် အသုံးများသည့် အခေါ်အဝေါ်များ၊ အယူအဆများကို အဓိပ္ပါယ် ဖွင့်ဆိုမည်။ သင်ခန်းစာ အဆုံး၌ ဤအယူအဆများကိုယူ၍ နောက်သင်ခန်းစာရှိ မဲရုံစာရင်းကို အကျဉ်းချုံး (summarise) နိုင်မည်။

Data နှင့် ပတ်သက်သည့် အခေါ်အဝေါ်များ

Data များကို ဆန်းစစ်ရာတွင် အသုံးများသည့် ခေါ်အဝေါ်တချို့ကို သင်ယူခြင်းဖြင့် စတင်ပါမည်။

သီးခြားယူနစ် (Observation)

Dataset တစ်ခုတွင် သီးခြားယူနစ် (individuals) များအကြောင်း သတင်းအချက်အလက်များ ပါဝင်သည်။ ဤသီးခြားယူနစ် တစ်ခုကို “observation” သို့မဟုတ် “case” ဟုခေါ်သည်။ Dataset အများစုရှိ row တစ်ခုစီတွင် individual များအကြောင်း သတင်းအချက်အလက်များပါဝင်သည်။ Module 1 တွင် ကျွန်ုပ်တို့ မဲရုံစာရင်းကို လေ့လာခဲ့ကြသည်။ ယင်း dataset ရှိ row တစ်ခုစီတွင် မဲရုံတစ်ခုချင်းအကြောင်း သတင်းအချက်အလက်များပါရှိသည်။

ကိန်းရှင် (Variable)

သီးခြားယူနစ် (observation) ၏ မည်သည့် ဝိသေသ လက္ခဏာကို မဆို ကိန်းရှင် (variable) ဟုခေါ်သည်။ လိင်၊ အလုပ်အကိုင် ကဲ့သို့သော ကိန်းရှင် (variable) များသည် individuals များကို ကဏ္ဍများတွင် ထည့်ပေးသည်။ အရပ်အမြင့်နှင့် မှတ်ပုံတင်ထားသည့် မဲဆန္ဒရှင်များကဲ့သို့ အခြား variable များမှာ တွက်ချက်နိုင်သည့် ကိန်းဂဏန်းတန်ဖိုးများပါရှိသည်။ နောက်တစ်ခုအနေဖြင့် data အမျိုးအစားများကို လေ့လာကြည့်မည်။

အချက်အလက် အမျိုးအစားများ

အချက်အလက်များကို ပုံစံအမျိုးမျိုးဖြင့် သိမ်းထားလေ့ရှိသည်။ ယင်းအမျိုးအစားများကို တစ်ခါတစ်ရံတွင် တိုင်းတာမှုအဆင့် (level of measurement) ဟုလည်း ရည်ညွှန်းခေါ်ဆိုတတ်ကြသည်။ ကျွန်ုပ်တို့ အနေဖြင့် data အမျိုးအစားများကို နားလည်ရန် လိုအပ်သည်၊ သို့မှသာ ယင်းတို့ကို ကောင်းမွန်စွာ အနှစ်ချုပ်နိုင်မည်။ Data အများအစား ၃ မျိုးရှိသည်။

၁။ Categorical သို့မဟုတ် Nominal ။ ဤ အချက်အလက်များတွင် ကဏ္ဍအမျိုးမျိုးရှိပြီး ကိန်းဂဏန်း အမျိုးအစား မဟုတ်သော အချက်များ ဖြစ်သည် (ဥပမာ လိင်၊ လူမျိုးစု၊ မဲဆန္ဒနယ် စသည်ဖြင့်)။ ဥပမာ ရွေးကောက်ပွဲ စောင့်ကြည့် လေ့လာရေး ပုံစံဖောင်တစ်ခုတွင် “သင်သည် တစ်နေ့လုံး လေ့လာ စောင့်ကြည့်ခွင့် ရခဲ့ပါသလား”စသည်ဖြင့် မေးနိုင်ပြီး အဖြေမှာလည်း (ရသည်) Yes သို့မဟုတ် (မရ) No သာ ဖြစ်သည်။ ရွေးကောက်ပွဲစီမံကျင်းပရေးအဖွဲ့ (EMB) တစ်ဖွဲ့သည် မဲရုံတစ်ရုံစီ၌ တာဝန်ကျသည့် ဝန်ထမ်းစာရင်းကို ထုတ်ပြန်နိုင်သည်၊ ယင်းစာရင်းတွင် ဝန်ထမ်းတစ်ဦးချင်းစီ၏ အမည်၊ ရာထူးတို့ ပါနိုင်သည်။ “ရာထူး” ဟူသည့် variable သည် categorical data သာလျှင်ဖြစ်နိုင်သည် (ဥပမာ ဥက္ကဌ၊ ဒုဥက္ကဌ၊ အတွင်းရေးမှုး စသည်ဖြင့် )။
၂။ Ordinal ။ ဤ အချက်အလက်များမှာ အစဉ် တစ်ခုခုသို့မဟုတ် အဆင့်တစ်ခုခုသို့ ဝင်ရောက်သည့် ကဏ္ဍများပါရှိသည့် အချက်အလက်များဖြစ်သည်။ ဥပမာ ရွေးကောက်ပွဲ စောင့်ကြည့်လေ့လာရေး ပုံစံဖောင် အတော်များများတွင် မဲပေးရန် လူမည်မျှကို ကူညီပေးခဲ့သနည်း စသည့်မေးခွန်းများပါနိုင်ပြီး အဖြေတွင် “မည်သူ တစ်ဉီးတစ်ယောက်ကိုမှ မကူညီခဲ့”(None)၊ “လူအနည်းငယ်ကို ကူညီခဲ့သည်”(Few) ၊ “လူတချို့ကို ကူညီခဲ့သည်”(Some)၊ “လူအတော်များများကို ကူညီခဲ့သည်”(Many) ၊ စသည်တို့ပါနိုင်သည်။ ဤနေရာတွင် “Many” သည် “Some” ထက်ပိုများ၍ “Some” မှာ “None” ထက်ပိုများသည်။
၃။ Continuous သို့မဟုတ် Interval ။ ဤ data အမျိုးအစားတွင် ကိန်းဂဏန်း အစဉ်အတန်းလိုက် ပါဝင်သည်။ Data value အားလုံး ဖြစ်နိုင်သည်။ ဥပမာအားဖြင့် ရွေးကောက်ပွဲနေ့ စောင့်ကြည့် လေ့လာရေး ပုံစံဖောင်တစ်ခုတွင် မဲရုံတစ်ရုံချင်းစီအတွက် မှတ်ပုံတင်ထားသူ မဲဆန္ဒရှင် စုစုပေါင်းနှင့် ကိုယ်စားလှယ်တစ်ဦးချင်းစီ ရရှိသည့် မဲအရေအတွက် စသည်တို့ကို မေးနိုင်သည်။

Variable (ကိန်းရှင်) တစ်ခုသည် မည်သည့် data အမျိုးအစားဖြစ်သည်ကို ပထမဦးစွာ နားလည်ထားခြင်းဖြင့် ၄င်း variable ကို မည်ကဲ့သို့ဖော်ပြမည်၊ မည်ကဲ့သို့ အနှစ်ချုပ်မည်ကို ဆုံးဖြတ်နိုင်သည်။

အချက်အလက်များကို ဖော်ပြခြင်းနှင့် အနှစ်ချုပ်ခြင်း

အဘယ်ကြောင့် အချက်အလက်များကို အနှစ်ချုပ် ကြသနည်း။ အချက်အလက်များကို ရိုးရှင်းစေရန်နှင့် အချက်အလက်ထဲတွင် ပုံမှန်ဟု ထင်ရသည့်အရာ၊ ပုံမှန်မဟုတ်ဟု ထင်ရသည့်အရာများကို ဖော်ထုတ်ရန် အလို့ငှာ အနှစ်ချုပ်ရသည်။ Variable (ကိန်းရှင်) များ၏ ဖြန့်ကျက်နေမှုသည် ယင်း variable (ကိန်းရှင်) တို့တွင် မည်သည့် တန်ဖိုးများပါရှိသည်၊ ယင်းတန်ဖိုးများကို အကြိမ်မည်မျှ ပါရှိသည် စသည်တို့ကို ပြသသည်။

အချက်အလက်များ၏ ဖြန့်ကျက်နေမှုကို ဖော်ပြရန် အသုံးအဝင်ဆုံးနည်းလမ်းနှစ်ခုမှာ

၁။ The typical (သမာရိုးကျပုံစံ)။ အချက်အလက်များ၏ ဗဟို သို့မဟုတ် အလယ်ကို ဖော်ပြသည်။ ယခုကဲ့သို့ ဗဟိုကို ဖော်ပြသည့်နည်းကို “measure of central tendency”(ဗဟိုညွှတ်ကိန်း အတိုင်းအတာ) ဟူ၍လည်းခေါ်သည်
၂။ The spread of the values around the center (ဗဟိုအနီးအနားတဝိုက်တွင် အချက်အလက်များ ဖြန့်ကျက်မှု)။ ဤနည်းသည် ဗဟိုနားတဝိုက်တွင် data များ မည်မျှ သိပ်သည်းစွာ ဖြန့်ကျက်နေကြောင်းကို ဖော်ပြသည်။ “measure of dispersion” ဟုလည်း ခေါ်သည်။

ဤကဲ့သို့ အချက်အလက်များအား ဖော်ပြသည့် နည်းလမ်းနှစ်သွယ်အား descriptive statistics ဟူ၍လည်း ရည်ညွှန်းခေါ်ဆိုသည်။

၁။ ဗဟို။ သမာရိုးကျ ဖြစ်မှု (typical) ဟူသည်အဘယ်နည်း။ (Central Tendencies)

ဗဟိုကိုကြည့်သည့် နည်းလမ်း ၃ ခုမှာ average (ပျမ်းမျှတန်ဖိုး) (mean ဟူ၍လည်းခေါ်သည်)၊ mode (ကြိမ်များကိန်း) နှင့် median (အလယ်ကိန်း) တို့ဖြစ်ကြသည်။ ဤ ၃ ခုလုံးသည် variable (ကိန်းရှင်) တစ်ခု၏ စံတန်ဖိုး (average)၊ ကြိမ်ရေ အများဆုံး ထပ်၍ကျသည့် ကိန်းဂဏန်း (mode) သို့မဟုတ် dataset တစ်ခုအတွင်းရှိ ကိန်းဂဏန်း အားလုံး၏ အလယ်တွင် ရှိသော ကိန်း (median)^[1] စသည်တို့ကိုဖော်ပြ၍ အချက်အလက်များ၏ ဖြန့်ဖြူးမှုကို အနှစ်ချုပ်ပြနိုင်သည်။ Average (ပျမ်းမျှတန်ဖိုး) သည် interval/ continuous အမျိုးအစား အချက်အလက် များအတွက် ဗဟိုကို တိုင်းတာရန် အသင့်တော်ဆုံးဖြစ်သည် (ဥပမာ မှတ်ပုံတင်ထားသည့် မဲဆန္ဒရှင် အရေအတွက်)။ Average (ပျမ်းမျှတန်ဖိုး) ကိုတွက်ရန် variable တစ်ခုအတွက် ကိန်းဂဏန်းအားလုံးကိုပေါင်း၍ အရေအတွက်အတွက်နှင့်စားသည်။ တစ်နည်းအားဖြင့်ပြောရလျှင် average (mean) သည် စုစုပေါင်းကို အရေအတွက်နှင့်စားခြင်းပင်။

ရိုးရှင်းသည့် ဥပမာ

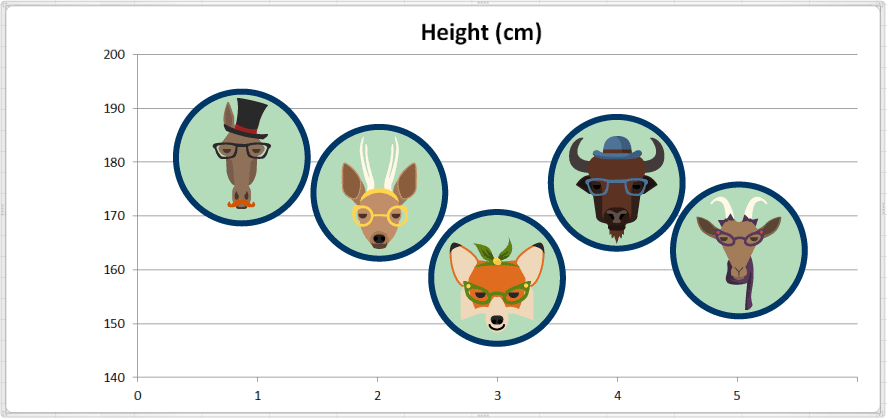
အောက်ပါ dataset ရှိ ဥပမာတွင် တိရစ္ဆာန်တချို့၏အမည်များနှင့်ဆက်စပ်သည့် အချက်အလက်များရှိသည်။ တိရစ္ဆာန် တစ်ကောင်းချင်းစီ၏ အမြင့် အတိုင်းအတာများလည်း ရှိသည်။ Dataset တွင် variable (ကိန်းရှင်) ၂မျိုး (အမည်နှင့် အမြင့်) နှင့် observation (သီးခြားယူနစ်) ၅ ခုရှိသည်။ dataset ကိုအောက်ပါအတိုင်းတွေ့နိုင်သည်။

ဤနေရာတွင် တိရစ္ဆာန်တစ်ကောင်ချင်းစီ၏ အမြင့်ကိုဖော်ပြထားသည့် ပုံချပ်ကိုပါ ဆွဲပေးထားသည်။

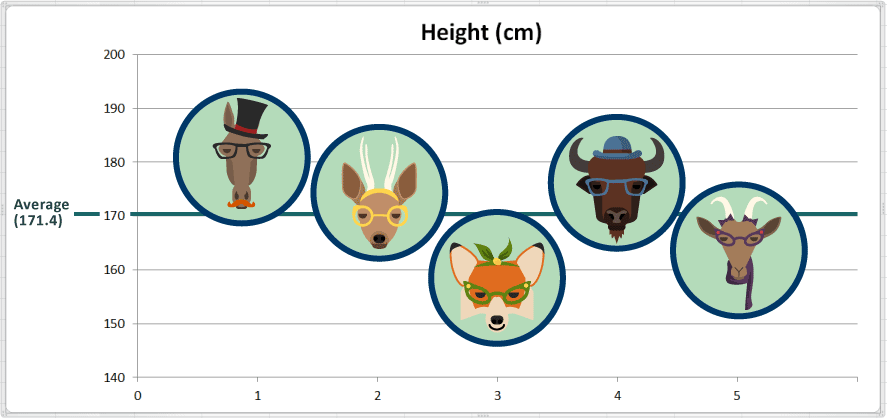
ပျမ်းမျှအမြင့် (average height) ကိုတွက်ရန် တန်ဖိုးများအားလုံးကိုပေါင်း၍ observation (သီးခြားယူနစ်) အရေအတွက်နှင့် စားသည်။

ပျမ်းမျှအမြင့် = (၁၈၁ + ၁၇၅ + ၁၅၉ + ၁၇၇ + ၁၆၅) ÷ ၅ = ၈၅၇ ÷ ၅ = ၁၇၁.၄

အမြင့်အတွက် ပျမ်းမျှတန်ဖိုးမှာ ၁၇၁.၄ စင်တီမီတာဖြစ်သည်။ ဤနေရာ၌ ကျွန်ုပ်တို့၏ ပျမ်းမျှသည် ပုံချပ်ပေါ်တွင် မည်သည့်ပုံပေါ်ကြောင်းမြင်နိုင်ရန် ရည်ညွှန်းမျဉ်းတစ်ကြောင်းထည့်ပေးထားသည်။

၂။ ဖြန့်ကျက်မှု။ ဗဟိုအနီးအနားတစ်ဝိုက်တွင် အချက်အလက်များကို မည်ကဲ့သို့ ပျံ့ကြဲနေသနည်း။ (measures of dispersion)

Data ဖြန့်ဖြူးမှု၏ ဖြန့်ကျက်နေမှုကို ကြည့်ခြင်းအားဖြင့် ယင်း အချက်အလက်အတွင်း ပြောင်းလဲမှု ပမာဏ၊ ကွဲပြားမှု ပမာဏကို သိနိုင်သည်။ ဖြန့်ကျက်မှု အတိုင်းအတာ ၃ ခုမှာ range (တာ)၊ standard deviation (စံသွေဖည်ကိန်း) နှင့် variance (ကွဲလွဲချက်) တို့ဖြစ်ကြသည်။

တာ (Range)

ဤသည်မှာ အကြီးဆုံးနှင့် အသေးဆုံးတန်ဖိုးများ၏ ကွာခြားမှု ဖြစ်သည်။ အစွန်းနှစ်ဖက်ကြား အကွာအဝေး ဖြစ်သည်။ Range ကိုတွက်ရန် အများဆုံးတန်ဖိုးကို ယူ၍ ၄င်းမှ အနိမ့်ဆုံးတန်ဖိုးကို နှုတ်သည်။

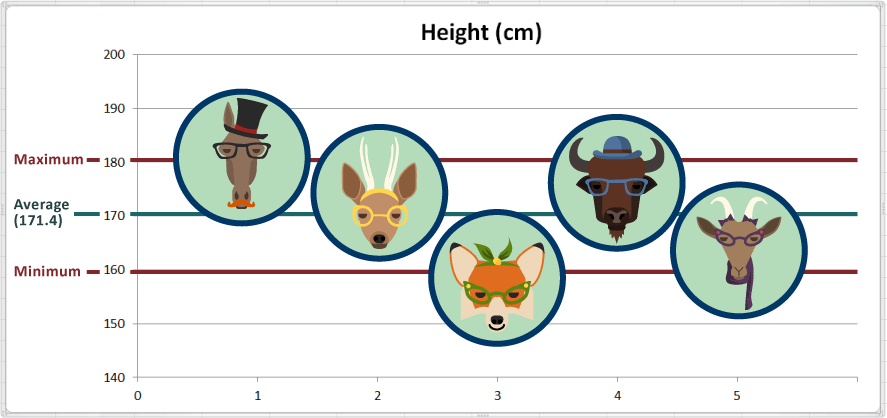
ကျွန်ုပ်တို့၏ အမြင့် dataset တွင် အကြီးဆုံးတန်ဖိုးမှာ 181 cm ဖြစ်သည်။
အနိမ့်ဆုံး တန်ဖိုးမှာ 159 cm ဖြစ်သည်။
အရပ်အမြင့် dataset ရှိ range မှာ 181 - 159 = 22 cm ဖြစ်သည်။
အများဆုံးနှင့်အနည်းဆုံးတို့ကိုညွှန်ပြရန် ရည်ညွှန်း မျဉ်းများ ထည့်ပေးထားသည်။

လက်တွေ့ကျကျပြောရလျှင် အမြင့်ဆုံးတန်ဖိုးနှင့် တိရစ္ဆာန်မှာ အရပ်အမြင့်ဆုံးဖြစ်ပြီး အနိမ့်ဆုံးတန်ဖိုးနှင့် တိရစ္ဆာန်မှာ အရပ်အနိမ့်ဆုံး ဖြစ်သည်။ ထို့ကြောင့် Harry ဟုခေါ်သည့် မြင်းမှာ အမြင့်ဆုံးဖြစ်ပြီး Fran ဟုခေါ်သည့် မြေခွေးမှာ အပုဆုံးဖြစ်သည်။

Range သည် အဆုံးမှတ်များ (အစွန်များ) ကိုပြသော်လည်း ယင်းအဆုံးမှတ်များအကြား အချက်အလက်များ သည် မည်၍မည်မျှ စိပ်ကြောင်း/ကျဲကြောင်း မပြသပေ။ ထို့ပြင် အချက်အလက်အများစုမှာ ပျမ်းမျှ နှင့် နီးသလား၊ အများဆုံးနှင့် နီးသလား၊ အနည်းဆုံးနှင့် နီးသလား လည်းမသိနိုင်ပေ။ ကျွန်ုပ်တို့၏ ပုံချပ်တွင် ကြည့်လျှင် တိရစ္ဆာန်များ၏ တစ်ဝက် ကျော်ကျော်ခန့် သည် အရပ်မြင့်ကြောင်း (ပျဉ်းမျှ အရပ်ထက်ပိုမြင့်) တွေ့နိုင်သည်။

အခြား ဖြန့်ကျက်မှု အတိုင်းအတာ (measures of dispersion) များဖြစ်သည့် variance (ကွဲလွဲချက်) နှင့် standard deviation (စံသွေဖည်ကိန်း) တို့က ဤမေးခွန်းများအတွက် အဖြေပေးနိုင်သည်။ ဤအတိုင်းအတာများသည် အချက်အလက်များ ဖြန့်ကျက်နေမှုကို ကိန်းဂဏန်းဖြင့် အကျဉ်းချုပ်ပေးနိုင်သည်။

စံသွေဖည်ကိန်း (Standard Deviation)

စံသွေဖည်ကိန်း (Standard deviation) သည် ပျမ်းမျှနှင့် နှိုင်းယှဉ်လျှင် မည်သည့် အချက်အလက်သည် ပုံမှန် ဖြစ်ခြင်း^[2] ရှိ၊မရှိ သိနိုင်သည့် နည်းလမ်း ဖြစ်သည်။ Standard deviation ၏ အလွန်အသုံးဝင်သည့် ဝိသေသတစ်ခုမှာ ၄င်းကို ဖော်ပြသည့် ယူနစ်မှာ အချက်အလက်ကိုဖော်ပြသည့် ယူနစ်နှင့် တူညီခြင်းပင်ဖြစ်သည်။ Standard deviation သည် ပြောင်းလဲမှုအညွှန်း (index of variability) တစ်ခုနှင့် အလားတူသည်။ အကြောင်းမှာ ၄င်းသည် အချက်အလက်များ ဖြန့်ကျက်မှုနှင့် အချိုးကျ၍ဖြစ်သည်။ Standard deviation ၏ တန်ဖိုးသည် ပျံ့နှံ့မှုများသည့်အခါ၊ (အချက်အလက်များ၏ တန်ဖိုးမှာ တစ်ခုနှင့် တစ်ခု ကွာခြားမှု ကြီးမားသည့်အခါ) ပို၍ ကျဲသည့် အခါ တန်ဖိုး ပို၍ကြီးသည်။ ပို၍ စိတ်သည့် ပျံ့နှံ့မှုများအတွက် (အချက်အလက်များ၏ တန်ဖိုးမှာ တစ်ခုနှင့် တစ်ခု သိပ်မကွာ သည့်အခါ) standard deviation ၏ တန်ဖိုးမှာ ပို၍ ငယ်သည်။

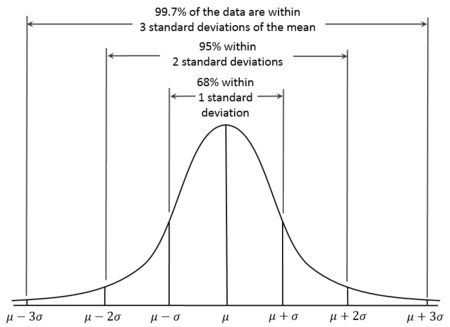
Standard deviation သည် ကိန်းရှင် (variable) တစ်ခု၏ ဖြန့်ကျက်မှုကို နားလည်ရန်အတွက် အလွန်အသုံးဝင်သည်။ ပုံမှန် ပျံ့နှံ့နေသည့် အချက်အလက်များအတွက် တန်ဖိုးအားလုံးနီးပါးသည် ယေဘုယျအားဖြင့် ပျမ်းမျှတန်ဖိုး (average) ၏ standard deviation ၃ ခုအတွင်းမှာပင်ရှိလိမ့်မည်။ စာရင်းအင်းပညာတွင် ဤအချက်ကို 68-95-99.7 စည်းမျဉ်း ဟူ၍ ရည်ညွှန်းပြောဆိုကြသည်။ 68.7 ရာခိုင်နှုန်းခန့်သည် average (ပျမ်းမျှ) ၏ standard deviation (mean) တစ်ခုအတွင်းကျရောက်သည်။ ထိုနည်းတူစွာ 95.45 ရာခိုင်နှုန်းခန့်သည် mean ၏ standard deviation ၂ ခုအတွင်းကျရောက်သည်။ 99.73 ရာခိုင်နှုန်းနီးပါးသည် mean ၏ standard deviation ၃ ခုအတွင်းကျရောက်သည်။

Wikipedia မှ 68-95-99.7 စည်းမျဉ်းကို ဖော်ပြသည့် ပုံတစ်ပုံ

လေ့ကျင့်ခန်း (၃) တွင်၂၀၀၈ မဲရုံစာရင်းမှ data များကို summarise လုပ်ရန် Excel ကို အသုံးပြုခဲ့ကြသည်။

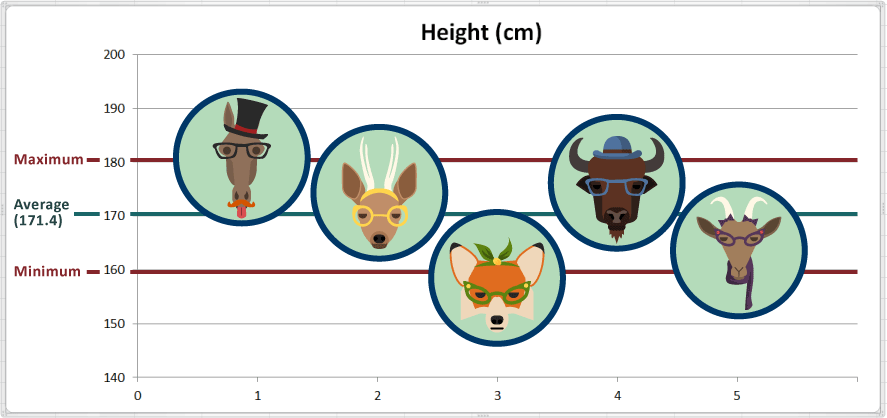
တိရစ္ဆာန်များ၏ အမြင့် dataset တွင် အမြင့်အတွက် standard deviation ကို တွက်ထားပြီးပြီ။ 9.1 cm ရသည်။^[3] ပျမ်းမျှ (Average) ၏ standard deviation ၃ ခုအတွင်း ကျရောက်နိုင်သည့် data များကိုပြရန် ပုံချပ်၏ သက်ဆိုင်သည့်နေရာများကို အရိပ်ခြယ်ထားပေးသည်။ ဤ range အတွင်း ကျရောက်သည့် အချက်အလက် များသည် ပုံမှန်ဖြစ်သည်။

Standard deviation က ကျွန်ုပ်တို့အား ပုံမှန်ဖြစ်သော အချက်အလက်၊ အလွန်ကြီးမားသော အချက်အလက်၊ အလွန်သေးငယ်သော အချက်အလက် စသည်တို့ကို သိနိုင်သည့် ပုံသေနည်းတစ်ခုကိုပေးသည်။ မြေခွေး Fran သည် အရပ်ပုကြောင်း ကျွန်ုပ်တို့ သိသည်။ Standard deviation နှင့် တန်ဖိုးများအားလုံးနီးပါး (99.73%) သည် standard deviation ၃ ခုအတွင်းကျရောက်ကြသည် ဟူသည့်အချက်တို့ကိုထောက်၍ Fran သည် အရပ်ပုသော်လည်း သာမန်ထက်လွန်၍ ပုခြင်းကား မဟုတ်ကြောင်း ကောက်ချက်ချနိုင်သည်။

ကွဲလွဲချက် (Variance)

စံသွေဖည်ကိန်း (Standard deviation) ကဲ့သို့ပင် ကွဲလွဲချက် (variance) သည်လည်း ပျမ်းမျှ အနီးအနားတစ်ဝိုက်တွင် ကိန်းဂဏန်းများ ပျံ့နှံ့နေမှုသည် မည်မျှစိပ် သို့မဟုတ် မည်မျှကျဲကြောင်းကို တိုင်းတာသည်။ ထို့ကြောင့် variance ကြီးခြင်းက data များသည် ပျမ်းမျှတန်ဖိုး (average) မှ အဝေးသို့ ဖြန့်ကျက်နေဟု ဆိုလိုပြီး variance ငယ်ခြင်းမှာ အချက်အလက်များသည် ပျမ်းမျှတန်ဖိုး (average) နားတစ်ဝိုက်တွင် ဖြန့်ကျက်နေသည်ဟု နားလည်ရမည်။ Variance သည် ပျမ်းမျှမှ ကိန်းဂဏန်း တစ်ခုစီ၏ ဆတိုးခြားနားခြင်းများကို ပျမ်းမျှရှာထားခြင်းပင်ဖြစ်သည် (အောက်တွင် သင်္ချာ ပုံသေနည်းကို ပေးထားသည်)။ ယခု သင်ခန်းစာတွင် ဤပုံသေနည်းကို အဓိကသင်ကြားမည်မဟုတ်သော်လည်း variance သည် standard deviation တွက်ခြင်း၏ အခြေခံအုတ်မြစ်ဖြစ်ကြောင်းတော့ နားလည်သဘောပေါက်ထား သင့်သည်။

သင့်ကိုယ်သင် စာမေးပွဲစစ်ကြည့်ပါ။

အောက်ပါမေးခွန်းများကို ဖြေခြင်းဖြင့် သင်ဗဟုသုတကို စစ်ဆေးကြည့်ပါ။

၁။ Observation ဟူသည် အဘယ်နည်း။
၂။ “Obervation” နှင့် “variable” အခေါ်အဝေါ်နှစ်ခုသည် တစ်ခုနှင့်တစ်ခု မည်ကဲ့သို့ ဆက်စပ်နေသနည်း။
၃။ Dataset များကို ဖော်ပြခြင်းသို့မဟုတ် အနှစ်ချုပ်ခြင်း၏ ရည်ရွယ်ချက်က အဘယ်နည်း။
၄။ Levels of measurement ဟူ၍လည်းခေါ်သည့် အချက်အလက် အမျိုးအစား ၃ မျိုးက မည်သည်တို့နည်း။
၅။ အချက်အလက်များ ဖြန့်ဖြူးမှုကို ဖော်ပြရန် အသုံးအဝင်ဆုံး နည်းလမ်း (၂) ခု ကို ရေးပြပါ။
၆။ မြေခွေး Fran သည် သာမန်ထက်လွန်၍ အရပ်ပုသလား။

အချက်အလက်များနှင့် ဆော့ကစားခြင်း

သင်ကိုယ်တိုင် တွက်ချက်မှုများ ပြုလုပ်လိုလျှင် အမြင့်နှင့်ဆက်စပ်သည့် dataset ကို ဤနေရာတွင် ရယူပါ။ Data များကို တွက်ချက်မှု အချို့နှင့်အတူ Excel file သို့မဟုတ် Open Spreadsheets file အဖြစ်ရယူနိုင်ပါသည်။

သင်္ချာ ပုံသေနည်းများ

Math is Fun ဝက်ဆိုက်ရှိ Standard Deviation Formulas အခန်းတွင် ရှင်းပြထားသည့် standard deviation ပုံသေနည်း ၂ ခုမှာ အောက်ပါအတိုင်းဖြစ်သည်။

The Population^[4] Standard Deviation":

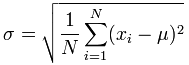
Formula 1

The Sample Standard Deviation":

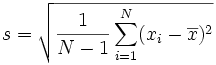
Formula 2

ကြည့်လိုက်လျှင် ရှုပ်ထွေးစရာကောင်းနေသည်။ သို့သော် အဓိက အပြောင်းအလဲမှာ Sample variance ကိုတွက်သည့်အခါ N-1 (N နှင့်မဟုတ်ဘဲ) နှင့် စားခြင်းဖြစ်သည်။ (Standard deviation သည် Variance ၏ square root ဖြစ်သည်ကိုသာ သတိချပ်ပါ၊ ထို့အတွက် variance ကိုတွက်သည့် formula မှာ square root မပါဘဲ အပေါ်က အတိုင်းပင် ဖြစ်ကြောင်း မှတ်သားပါ။

ကျေးဇူးတင်လွှာ

တိရစ္ဆာန်ဓါတ်ပုံများသည် Dashikka/Shutterstock ၏ မူပိုင်ဖြစ်သည်။

Median ကို တွက်ချက်ရန် ပုံသေနည်းမှာ “([စုစုပေါင်း အချက်အလက် အရေအတွက်] + ၁) ÷ ၂”ဟူ၍ ဖြစ်သည်။ သို့သော် သင့်အနေဖြင့် ထိုပုံသေနည်းကို အသုံးပြုရန် မလိုပါ။ ထိုအစား စာရင်း၏ အစမှ အလယ်မှတ် ရောက်သည်အထိ ရေတွက်သွားသည့် နည်းကိုလည်း သုံးနိုင်သည်။ ကြိမ်ရေအများဆုံး ကိန်းဆိုသည်မှာ အခြား ဂဏန်းများထက် ပို၍ ကြိမ်ဖန်များစွာ ပါဝင်သော ကိန်းဖြစ်သည်။ ဥပမာ ၂၊ ၃၊ ၄၊ ၅၊ ၄၊ ၄၊ ၆၊ ၁၀၊ ၁၂ ဟူသော ကိန်းစဉ်တွင် ကြိမ်ရေအများဆုံးကိန်း (mode) မှာ ၄ ဖြစ်သည်။ ↩︎
ပုံမှန်ဖြစ်ခြင်း ဆိုသည်ကို ဖြစ်တန်စွမ်းအား တွက်ချက်သည့် နည်းဖြင့် တွေးရန် လိုအပ်သည်။ ပုံမှန်ဖြစ်ခြင်းသည် အလွန် ဖြစ်နိုင်ချေရှိသော၊ ပုံမှန်ဖြစ်လေ့ဖြစ်ထ ရှိသော အရာကို ဆိုလိုသည်။ ↩︎
ယခုလေ့ကျင့်ခန်းတွင် စံသွေဖည်ကိန်း (standard deviation) တွက်နည်းကို ခေတ္တကျော်သွားမည်။ အကြောင်းမှာ standard deviation ၏ သဘောတရားကို နားလည်ရန် ရည်ရွယ်ပြီး တွက်နည်းများဖြင့် ရှုပ်မနေစေရန် ဖြစ်သည်။ standard deviation နှင့် variance တွက်ချက်သည့် ပုံသေနည်းများကို လေ့လာလိုသူများအတွက် ဤလေ့ကျင့်ခန်း အဆုံးတွင် ဖော်ပြပေးထားသည်။. ↩︎
“Population” ဆိုသည်မှာ dataset တစ်ခုလုံးကို (အချက်အလက်အားလုံး) ကို အနှစ်ချုပ်ခြင်း ဖြစ်သည်။ “Sample” (နမူနာ) ဆိုသည်မှာ dataset တစ်ခုလုံးထဲမှ နမူနာတချို့ကို ရွေးထုတ် တွက်ချက်ခြင်း ဖြစ်သည်။ ↩︎