1. Une Douce Introduction à la Synthèse de Données

Dans ce tutoriel, nous allons définir certains termes et concepts communs, y compris les types ou catégories de données. Ensuite, nous allons apprendre à décrire un ensemble de données. À la fin, vous serez prêt à approcher les concepts décrits ici et à les utiliser pour synthétiser la liste du bureau de vote dans le module suivant.

La Terminologie des Données

Nous commençons par apprendre quelques termes courants utilisés dans l'examen des données.

L'Observation

Un ensemble de données contient des informations sur «les individus.» Chaque «individu» est appelé «observation» ou «cas». Dans la plupart des ensembles de données, chaque ligne contient des informations sur un individu.

Les Variables

Toute caractéristique d'un individu (par exemple, l'observation) est appelée une variable. Certaines variables, comme le sexe et le titre de travail, place les individus dans des catégories. D'autres, comme la hauteur ou le nombre d'électeurs inscrits, prennent des valeurs numériques pour lesquels nous pouvons faire de l'arithmétique. Ensuite, nous allons jeter un coup d'œil aux différents types de données.

Types de Données

Les données sont classées sous différents types, qui sont parfois désignés comme «niveau de mesure.» Nous avons besoin de comprendre les types de données, car elles nous aident à comprendre comment les synthétiser correctement. Il y a trois types de données:

1. Catégorique ou nominale: Ce sont des données qui ont plusieurs catégories et ne sont pas numériques (par exemple, le sexe, l'origine ethnique, la circonscription). Par exemple, un formulaire d'observation des élections peut demander «Étiez-vous autorisé à observer toute la journée?», Où l'option de réponse est «Oui» ou «Non» Un organisme de gestion des élections (OGE) peut publier une liste des fonctionnaires qui sont affectés à chaque bureau de vote, et cette liste peut contenir le nom et le poste du fonctionnaire. La variable «poste» est susceptible d'être une donnée catégorique (par exemple, le président, le vice-président et secrétaire).
2. Ordinale: Ce sont des données avec des catégories qui ont un ordre ou un rang spécifique. Par exemple, sur de nombreux formulaires d'observation des élections, il y a une question qui demande: «Combien de personnes ont été assistées pour voter?» Où les options de réponse sont «Aucun», «Peu», «Quelques», ou «Beaucoup.» «Beaucoup» est plus que «Quelques», qui est plus qu' «Aucun».
3. Continu ou à Intervalle: Ce type de données dispose d'une gamme de nombres continues. Toutes les valeurs de données sont possibles. Par exemple, le formulaire d'observation le jour du scrutin peut demander le nombre d'électeurs inscrits dans chaque bureau de vote ou le nombre de votes reçus pour chaque candidat.

En comprenant dans un premier temps à quel type de données appartient une variable, nous pouvons alors décider de la meilleure façon de résumer ou de décrire cette variable.

Décrire et Résumer les Données

Pourquoi synthétisons-nous les données? Nous synthétisons les données pour «simplifier» les données et identifier rapidement ce qui semble «normal» et ce qui semble bizarre. La répartition d'une variable montre quelles valeurs prend la variable et à quelle fréquence la variable prend ces valeurs.

Les deux façons les plus utiles de décrire la distribution des données sont:

1. La typique Celle-ci décrit le centre - ou le milieu - des données. Cette façon de décrire le centre est aussi appelé une «mesure de la tendance centrale».
2. La dispersion des valeurs autour du centre: Celle-ci décrit la densité de distribution des données autour du centre. Elle est également appelé «mesure de dispersion.»

Ces deux façons de décrire les données sont aussi appelées statistiques descriptives.

1. Le Centre : Qu'est ce qui est Typique? (Tendances Centrales)

Les trois manières communes d'observer le centre sont la moyenne, le mode et la médiane. Elles résument toutes les trois une distribution de données en décrivant la valeur typique d'une variable (en moyenne), le nombre le plus fréquemment répété (mode), ou le nombre au milieu de tous les autres nombres dans un ensemble de données (médiane).^[1] Dans ce module, nous allons mettre l'accent sur la moyenne. La moyenne est la façon la plus appropriée pour mesurer le centre de données d'intervalle / continue (par exemple, nombre d'électeurs inscrits). Pour calculer la moyenne, on additionne tous les chiffres pour une variable, puis on divise par le nombre de chiffres qu'il y a. En d'autres termes la moyenne est la somme divisée par le nombre.

Exemple Simple

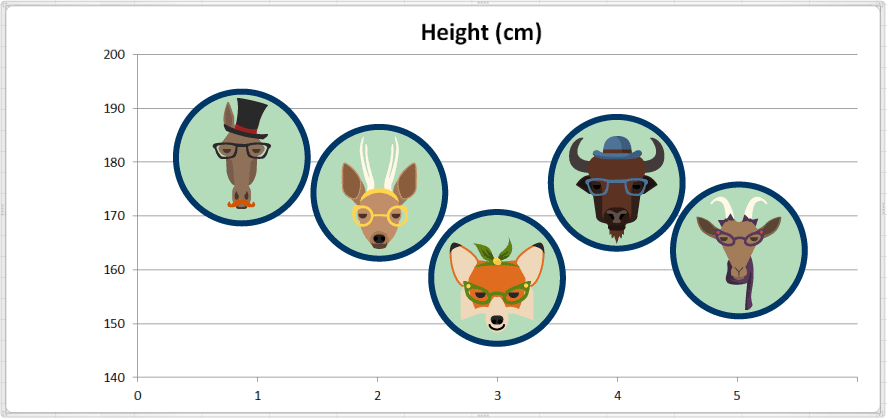
Dans l'exemple d'ensemble de données ci-dessous, nous avons des informations sur les noms de certains animaux. Nous avons également des mesures sur la taille de chaque animal. L'ensemble de données a deux variables - «name» and «height» («nom» et «taille») - et cinq observations. Voici l'ensemble de données:

Ici, nous avons fait un rapide tableau qui précise la taille de chaque animal:

Pour calculer la taille moyenne (en cm), on additionne toutes les valeurs et on les divise par nombre total d'observations.

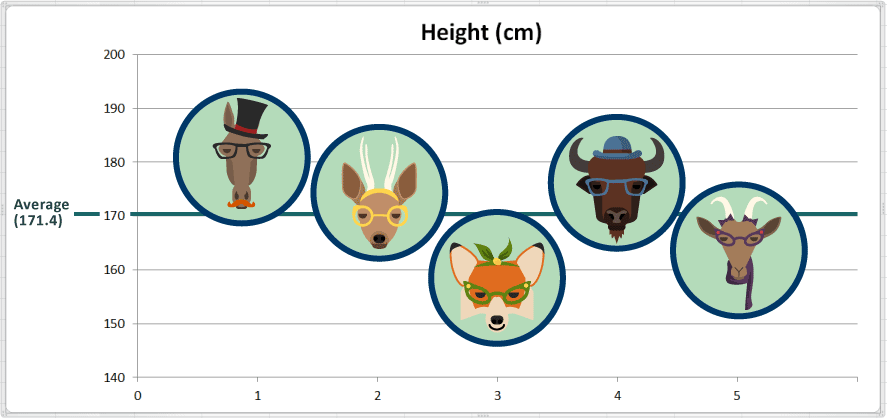
Taille Moyenne = (181 + 175 + 159 + 177 + 165) ÷ 5 = 857 ÷ 5 = 171.4

La valeur moyenne de la taille est de 171,4 centimètres. Ici, nous avons ajouté une ligne de référence indiquant la moyenne sur notre tableau de sorte que nous puissions voir à quoi cela correspond:

2. La Dispersion: Comment les données sont-elles distribuées autour du centre? (Mesures de Dispersion)

Observer l'étendue de la distribution des données nous indique le degré de variation, ou de diversité, parmi les données. Les trois mesures de dispersion des données sont l'étendue, l'écart-type et la variance.

L'Etendue

C'est la différence entre la plus grande et la plus petite valeur. Elle est la distance entre les extrêmes. Pour calculer l'étendue, nous prenons la valeur maximale que nous soustrayons à la valeur minimale.

Dans notre série de données sur la taille, quelle est la plus grande valeur («maximum»)? 181 cm
Dans le même exemple, quelle est la valeur la plus petite («minimum»)? 159 cm
L'étendue dans notre série de données sur la taille est 181-159 = 22 cm
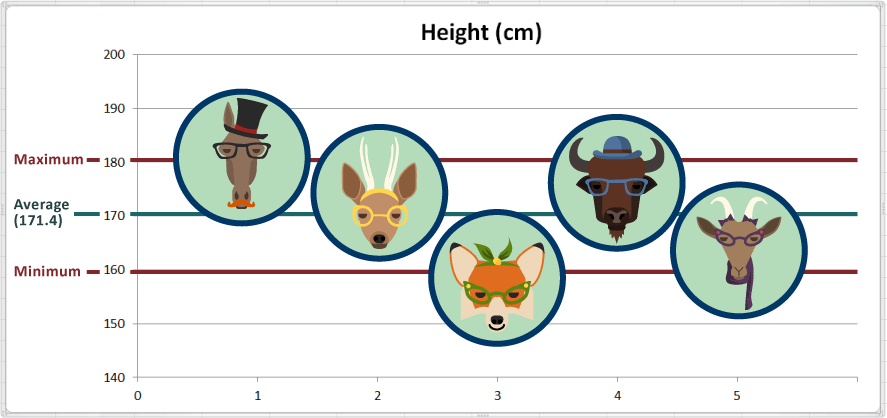
Ici nous avons ajouté quelques lignes de référence sur la carte pour indiquer le maximum («maximum») et minimale («minimale»):

En termes pratiques, l'animal avec la valeur maximale est le plus grand, et l'animal avec la valeur minimale est le plus petit. Donc Harry the Horse (Harry le Cheval) est le plus grand, et Fran the Fox (Fran la Renarde) est la plus petite.

Alors que l'étendue nous donne les critères d'évaluation (c.-à-d. extrêmes), elle ne nous dit rien sur la façon dont les données sont réparties (rapprochées ou dispersées) entre ces deux extrêmes. Nous ne savons pas non plus si les données sont plus proches de la moyenne, du maximum ou du minimum. A partir de notre tableau, il apparait qu'un peu plus de la moitié des animaux sont grands (c.-à.d., au-dessus de la hauteur moyenne).

Deux autres mesures connexes de la dispersion - la variance et l'écart type - peuvent nous aider à répondre à ces questions. Ils fournissent un résumé numérique sur le degré de dispersion des données.

L'Ecart-Type

L'écart-type («écart-type») nous fournit un moyen standard de savoir ce qui est normal^[2] compte tenu de la moyenne. Un attribut très utile de l'écart type est qu'il est exprimé dans les mêmes unités que les données elles-même. L'écart type est comme un indice de la variabilité, car il est proportionnel à la dispersion des données. L'écart type est plus grand pour des distributions diverses (c., les données sont largement dispersés). L'écart type est plus faible pour des distributions moins diverses (par exemple, les données sont regroupées).

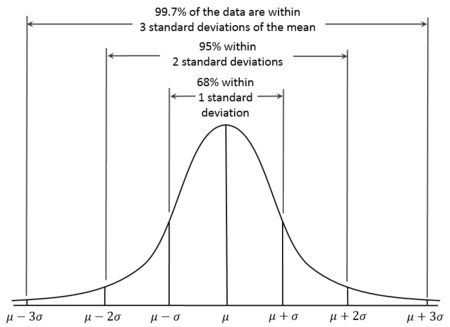
L'écart-type est très utile pour comprendre la répartition d'une variable. Pour la plupart des données normalement distribuées, généralement la quasi-totalité des valeurs aura un écart de trois écarts-types à la moyenne. Dans les statistiques, ce qui est parfois appelé la règle 68-95-99.7. 68,27% des valeurs se trouvent à moins d' 1 écart type de la moyenne (moyenne). De même, environ 95,45% des valeurs se situent à l'intérieur de deux écarts types de la moyenne. Presque toutes (99,73%) les valeurs se situent à trois écarts-types de la moyenne.

Un diagramme sur la règle 68-95-99.7 de wikipedia

Dans le Module 3, nous utilisons Excel pour résumer les données dans la liste des bureaux de vote de 2008.

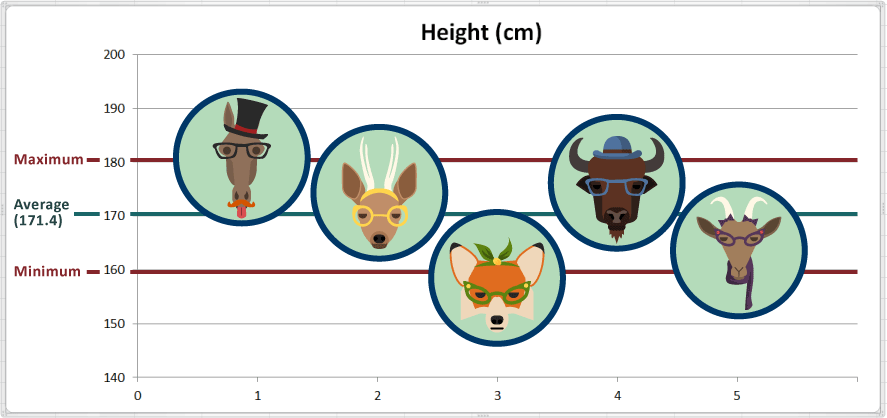
Dans l'échantillon sur la série de données sur la taille des animaux nous avons calculé l'écart-type pour les tailles. Il est de 9,1 cm.^[3] Sur le graphique, nous avons la zone ombragée pour montrer quelles sont les données comprises dans les trois écart-types (9.1 x 3) à la moyenne. Toutes les données dans cette distribution sont normales.

L'écart-type nous donne un moyen standardisé de savoir ce qui est normal, ce qui est extra-large ou ce qui est très petit. Nous savons que Fran the Fox (Fran la Renarde) est petite. Quand on considère l'écart-type et la quasi-totalité (99,73%) de toutes les valeurs sont généralement dans les 3 écarts-types, nous pouvons conclure que Fran est petite mais pas anormalement petite.

La Variance

Semblable à l'écart-type, la variance mesure la façon dont les nombres sont répartis autour de la moyenne. Ainsi, une plus grande variance signifie que les données sont réparties de manière plus éloignés de la moyenne, et si la variance est plus faible, les données sont plus étroitement regroupées autour de la moyenne. La variance est la moyenne des écarts au carré (ou les écarts) de chaque nombre à la moyenne (la formule mathématique est à la fin de cette note). On ne va pas se concentrer sur la formule dans ce module, mais il est important de comprendre que la variance fournit la base pour le calcul de l'écart-type.

Testez-Vous

Testez votre savoir en répondant aux questions:

1. Qu'est-ce qu'une observation?
2. Comment les concepts d' «observations» et de «variable» sont liés l'un à l'autre?
3. Quel est le but de décrire et résumer une série de données?
4. Quels sont les trois types de données (aussi appelés niveau de mesure)?
5. Listez les deux manières les plus utiles pour décrire la distribution des données?
6. Est-ce que Fran la Renarde est anormalement petite?

Jouez avec les Données

Si vous voulez effectuer vos propres calculs, voici la série de données sur la taille. Les données avec quelques calculs sont disponibles en Fichier Excel ou dans un Fichier de Calcul Ouvert.

Les Formules Mathématiques

Voici les deux formules pour l'écart-type, expliquées dans la section Formules des Ecart-Types sur le site Math is Fun (les Maths c'est amusant).

L'Ecart Type de Population^[4] «Standard Deviation»:

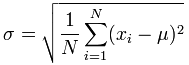
L'Ecart Type de l'Echantillon:

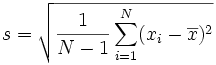
Cela semble compliqué, mais le changement important est de diviser par N-1 (à la place de N) lors du calcul de la variance de l'échantillon. (Rappelez-vous que l'écart-type est simplement la racine carrée de la Variance, donc la formule de calcul de la variance est la même formule que ci-dessus, mais sans la racine carrée.)

Crédits

Toutes les images d'animaux sont de l'auteur Dashikka/Shutterstock.

---

1. Pour trouver la médiane, la formule est «([le nombre de points de données] + 1) ÷ 2», mais vous n'avez pas à utiliser la formule. Si vous préférez, vous pouvez simplement compter à partir des deux extremités jusqu'à ce que vous rencontrez le milieu. Le mode est le nombre qui se répète le plus souvent dans une distribution. Dans une série de valeurs de 2, 3, 4, 5, 4, 4, 6, 10, 12; le mode est 4. ↩︎

2. Il est utile de penser à «normale» en termes probabilistes, où «normal» signifie quelque chose de très possible ou très typique. ↩︎

3. Nous passons le calcul de l'écart-type pour ce module, parce que nous voulons nous concentrer sur le concept plutôt que de se laisser prendre dans la formule. La formule pour l'écart-type et la variance sont à la fin de ce module pour ceux veulent les consulter. ↩︎

4. Le terme «population» signifie que vous résumez l'ensemble de la série de données. Le terme «échantillon» signifie que vous travaillez avec un petit sous-ensemble (ie, un échantillon) d'un ensemble de données plus vaste (population). ↩︎